
Trigonometry
Section by Section
It is a quite long page. You can go to categories only you want by links below.
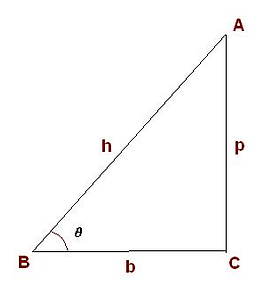
I am sure that all of you know what 'triangle' is. Am I right? How can you define triangle?. Think. The word has reason to be. Tri-angle. Three angles! Triangle is a plane figure which has three angles (corners) and three sides (edges). then, what kind of triangles do you know already? List as much as you can come up with. Acute triangle, obtuse triangle, isosceles triangle, equaliteral triangle, right triangle. This page is about 'trigonometry'. Among these triangles, what is working with it?
Trigonometry uses right triangle, that one of its triangle is right angle (90º). Let's look at one example above. Triangle ABC is a right triangle that the angle C is a right angle. Let's call the angle B as theta(Θ) The hypotenuse is sigment AB, which is the opposite side of right angle and the longest among three sides, sigment BC is the adjacent, and sigment AC is the opposite side of angle B, Θ.
The first step of trigonometry is 'Pythagorean Theorem'. Square of hypothenus is the sum of the square of rest two sides. Or, h²=b²+p². You may saw 'a²=b²+c²' somewhere. It's same thing, just using different letters for same things. Then, from this theorem, you can find that the length of hypothenus is √(b²+h²).
Let's go to the next step. Did you ever see something like 'sin' and 'csc'? These represent trigonometric ratios. There are three major ones;
--------------------------------------------------
sin (sine) = opposite/hypothenus
cos (cosine) = adjacent/hypothenus
tan (tangent) = opposite/adjacent
--------------------------------------------------
What is sinΘ for this triangle? Sin is opposite over hypothenus, so segment AC over segment AB.
Inverse
Besides, there are something called secant, cosecant and cotangent. What are they? They are the inverse of sine, cosine and tangent.
Secant (sec) is the inverse of cosine (cos), so we can say secΘ=1/cosΘ.
Cosecant (csc or cosec) is the inverse of sine (sin), cscΘ=1/sinΘ.
Cotangent (cot) is the inverse of tangent (tan), cotΘ=1/tanΘ.
Cot is quite easy to memorize, but sec and csc must be confusing. Here is an easy way. See the third letter. Secant 'C', which is cosine, cosecant 'S', which is sine. When you just read, you might think you get it, but you have to practice to make it your own.
Unit Circle/Exact Trig Values
Acute triangle | The triangle that its three angles are all acute angles. (smaller than 90º)
Obtuse triangle | The triangle that one of its angle is obtuse angle. (bigger than 90º and smaller than 180º)
isosceles triangle | The triangle that its two sides are same in length.
equaliteral triangle | The triangle that its three sides are all same and three angles are all same.
More about Pythagorean Theorem-CLICK
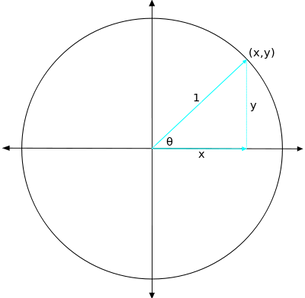
When we draw a right triangle on the plane coordinate, it is easy to get trigonometry ratios, especially for special angles. Draw a circle, radius of 1, center on the origin. This circle is called 'unit circle'. Then. choose any point on the circle. From that point, when you draw a straight segment to the origin. The length of it should be 1 because it is distance from a point on the circle to the center of the circle, the radius, 1. Then, draw a perpendicular line to the x-axis. Then, we get the right triangle, right? Let's call the angle between the radius and x-axis Θ. Also, we can find that the adjacent is x value of the point on the circle, and opposite is y. Now, we can find that;
-----------------------
sinΘ=y/1=y
cosΘ=x/1=x
tanΘ=y/x
-----------------------
What happen when Θ is 45º? Then, the triangle is isosceles right triangle, we can find x=y. Here, we can easily find x and y are all 1/√(2) or √(2)/2 because;
1²=x²+y²
1=2x²
1/2=x²
√(1/2)=x
x=1/√(2)=√(2)/2
We found x and y are 1/√(2) or √(2)/2. Here, we can find sinΘ and cosΘ, right? Because they are x and y. Simple!
*****
cos45º=1/√(2) or √(2)/2
sin45º=1/√(2) or √(2)/2
tan45º={1/√(2)}\{1/√(2)}=1
*****
What about Θ=30º?
Actually, this triangle is very interesing, so let's look closer.
perpendicular | making a right angle, 90º. verticle
Angle smaller than 0º or greater than 360º | On the unit circle, you can see that the angle start from the positive side of x axis and move anticlockwise. Therefore, when the angle is over 360º, you just have to go around more times. For example, when it is 390º, go all the way of the circle once, and 30º more. Than, you can see 390º=30º. When the angle is negative, go backwords, clockwise. Remember it always STARTS FROM POSITIVE SIDE OF THE X-AXIS.

When you look at the image above, you can find triangle ABD the equaliteral triangle when you draw a line that cuts the right triangle for 60º and 30º. Also, you can find that the triangle BCD is isosceles triangle because two angles are same. Finally, we can find that length of all sides marked on the image is same. What can you see now? Can't you see that AC is double length of AB.
When you think the triangle is on the unit circle, with Θ=30º.
*****
1²=(1/2)²+BC²
1²-(1/2)²=BC²
(3/4)=BC²
√(3/4)=BC
√(3)/2=BC
*****
x=√(3)/2
y=1/2
hypothenuse=1
By these values, we can easily find trig values.
-----------
sin30º=y=1/2
cos30º=x
=√(3)/2
tan30º=y/x=(1/2)/(√(3)/2)
=1/√(3)
=√(3)/3
-----------
Now, you can also find when Θ=60º because in that triangle above, one of the angle is 30º, but also the other one is 60º. The hypothenuse is 1, as 30º. When you rotate the triangle a bit, you can easily find x and y values too.
x=1/2
y=√(3)/2
Just x and y will switch with Θ=30º. Then, what happen to sin and cos? They will just switch each other too!
------------
60º
sin60º=√(3)/2
cos60º=1/2
tan60º={1/2}/{√(3)/2}
=1/√(3)
=√(3)/3
------------
For further question solving and deeper studies, you have to memorize these values. Remember. When you add squares of sin and cos values, you have to get 1 (square of hypothenuse).
QUADRANTs
With unit circle, there are more benefits, to find trig values of angle over 90 degrees. What will sin135º be? Can you guess?
Think.
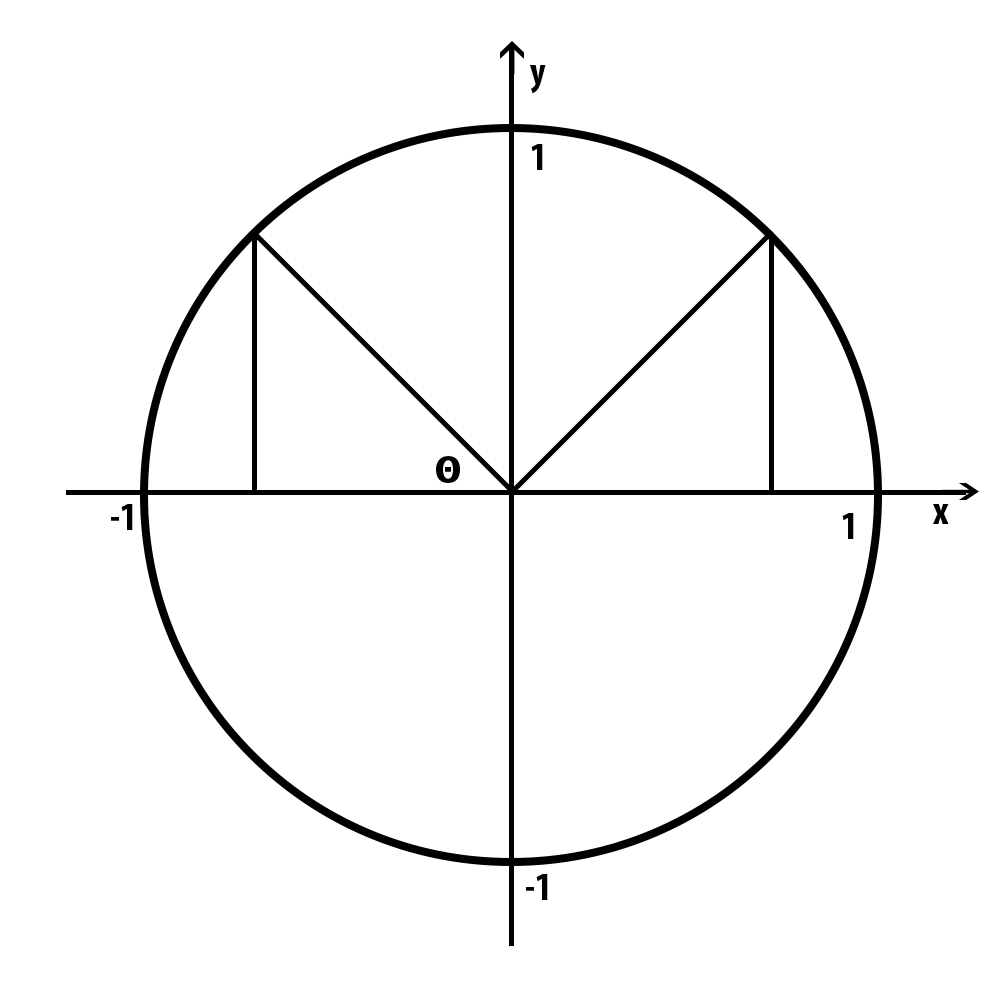
Okay. Here is the image. There is an angle Θ on the second quadrant. Let's compare with one on the first quadrant. We know that cosine value is x value, sine value is y value, and tangent value is y/x, which is the slope of hypothenus.
First, x value. When you say the x value of triangle on the first quadrant is x, how can you call the x value on the second quadrant? It reflects about the y axis, so only the sign changes. -x (nevative)!
Y value? First and second quadrant has same y value, so stay same.
Tangent, it is reflecting about the y axis, so it also changes the sign.
-----------
1st 2nd
cos x -x
sin y y
tan y/x -y/x
-----------
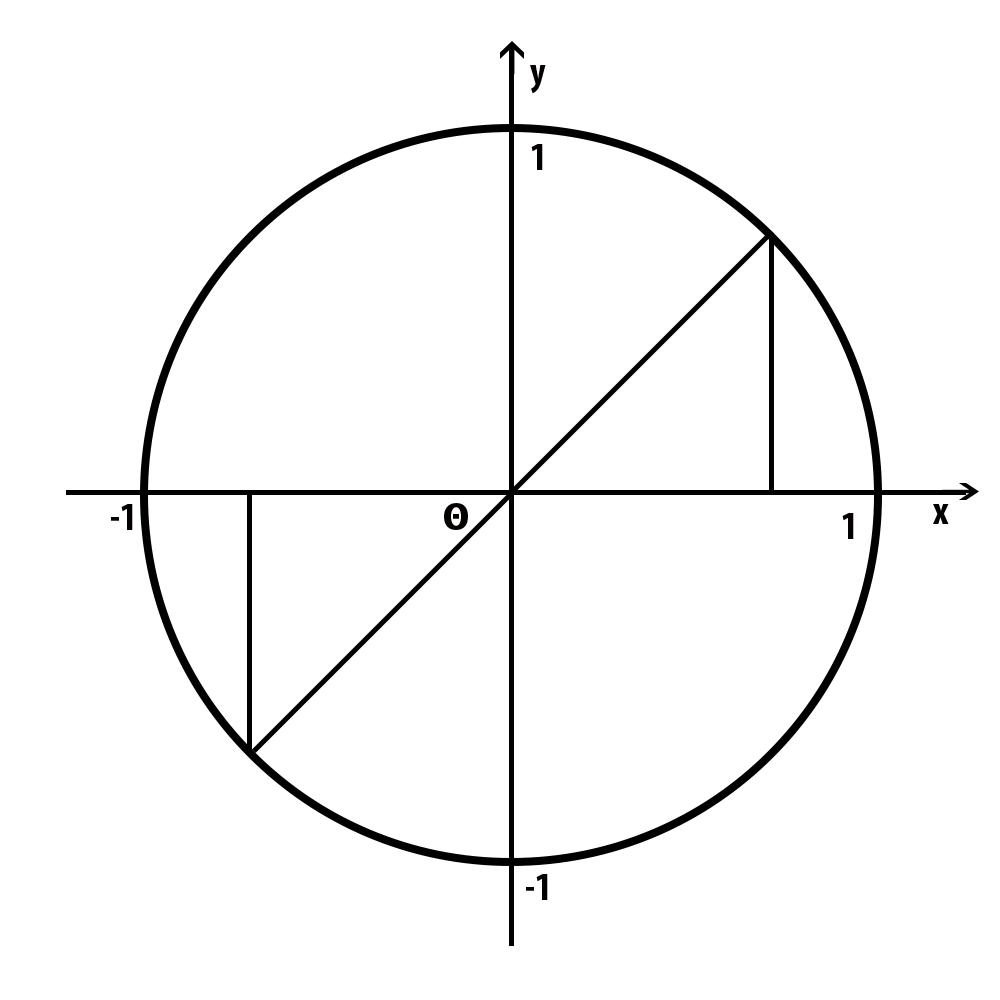
Now, the angle is on the third quadrant. What happen to x value? Negative. What about y value? also negative. What about the slope of hypothenuse? Stay same.
-----------
1st 2nd
cos x -x
sin y -y
tan y/x y/x
-----------
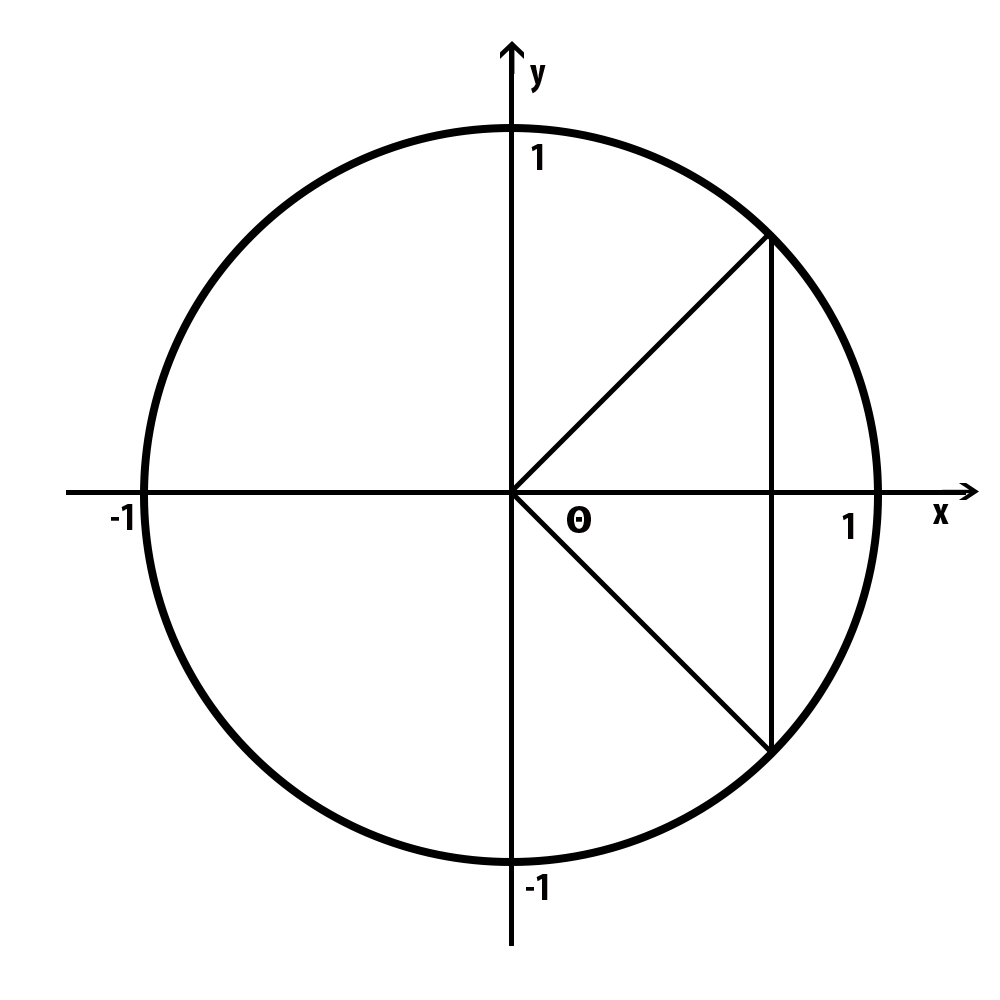
Lastly, 4th quadrants. What happen to x value on fourth quadrant? It stays same. Y value is opposite, changing the sign, and the sign of slope also changes.
-----------
1st 2nd
cos x x
sin y -y
tan y/x -y/x
-----------
Okay. When you just read descriptions, you think you get it, but when you are asked to answer 'what is sin225º?', you will be just, blank. So, many teachers give you the way to memorize, and it is quite benefitial. However, understand first and memorize. Understanding is the very first thing. Also, when you understand, it is much easier to memorize.
Okay, when you see the pattern, you can find that except first quadrant, other three have only one positive value, sine for 2nd Q, tangent for 3rd Q, and cosine for 4th Q, and all three on 1st Q.
1st, All, 2nd, Sin, 3rd, Tan, and 4th, Cos. A.S.T.C. There is some sentences might help you. All Students Take Calculus. This sentence doens't have any meaning, but just to memorize these four letters. A.S.T.C.
Got it? Got it!
Only one little point more.
You can see that all angles is the angle that the hypotenus and x-axis make. Not y-axis. Therefore, when the angle is on 2nd quadrant,
(if you have any questions, feel free to ask questions on this Facebook Page. I check it every day.)
Radians
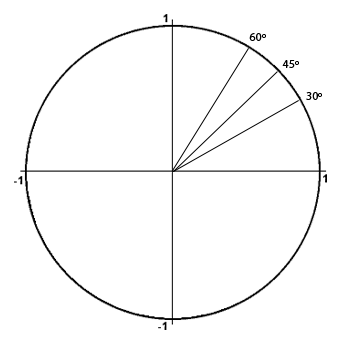
When you do trigonometry, at some point, you will find weird angle, not the degrees but something like π/2. What are they?
Okay. There are three ways to read angles. Degrees, what we all know, radians and gradian. That angle with π is called radian. Where did you see π before? When we find the area of circle or circumference, right? There you go. It is all about circumference of a unit circle. What is the circumference of a circle? 2πr (r=radius). Because radius of an unit circle is 1, circumference of it should be 2π. What is the angle of a complete circle? (Think as the value of Θ of the triangle on the unit circle) 360º. So, 360º=2π. Simple, right? Then, what will 180º be? Because it is half of 360º, it will be half of 2π, so π. Here, we can find the eaisiest one, we can easily find other angles too. 180º=π. Let's find other angles, then.
*****
180º=π
90º=π/2 (half of 180º)
45º=π/4 (half of 90º, one-fourth of 180º)
60º=π/3 (one-third of 180º)
30º=π/6 (half of 60º)
*****
Then, let's apply radians to the trigonometry!
What is sin(π/4)? So, we now know that π/4 is same as 45º. What is sin45º? It was 1/√(2) or √(2)/2. Therefore, sin(π/4) is 1/√(2) or √(2)/2. Easy, right? When you just know the radians, trigonometry of it is simple, just like degrees.
When you keep using radians, it can be easier than degrees because it is easier to see the rates with π. If the angle is really big like 1980º, it is hard to divide it in 360, but when it is 11π, it is much easier to see that it is same as π.
Graph
When you learned about polynomial equations, like quadratics, you had graph. Then, what happen when you graph trig values?
Before we actually look at the graphs, let's think about it first. Draw a unit circle in your mind. You already know that cos value is the x value and sin value is the y value of the point. What will be domain or range? For both cos and sin, they can't be bigger than 1 or smaller than -1 because the point is always on the unit circle. Then, we can find that range will be -1≤cos≤1 and -1≤sin≤1. What about domain? You now know the angle over 360 or smaller than 0 too, so domain can be any number.
*For trig graphs, we usually use radian instead degrees because the value of degree is too big; 360 degrees while y is from -1 to 1, but radians is 2π (6.28...) instead 360º. I will also use radians here.*
Now, look sin and cos separetely. First, sine graph.
Sine is y value. Domain from 0 to π/2, y value is positive number, and it increases. From π/2 to π, y is still positive, but it decreases. When x is from π to 3π/2, y value is negative, and still decreasing. From 3π/2 to 2π, it is still negative value but increases. You might understand better with the animation below.
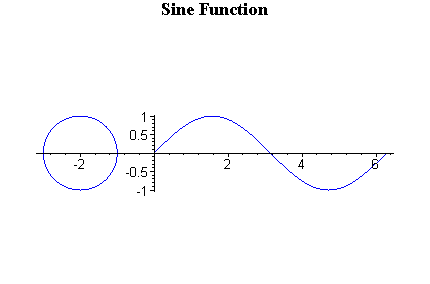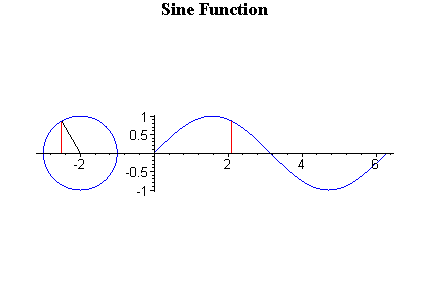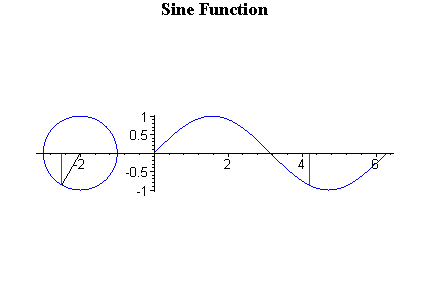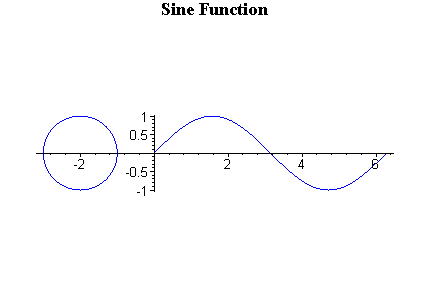
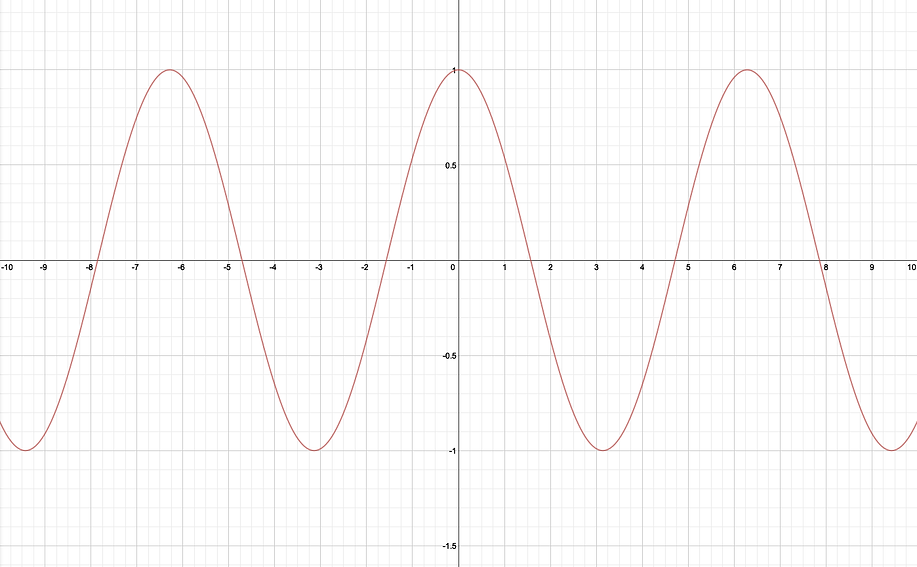
Because of this change, sin graph will look like above. The graph repeats and repeats because over 2π, sin value will be same as from 0 again.
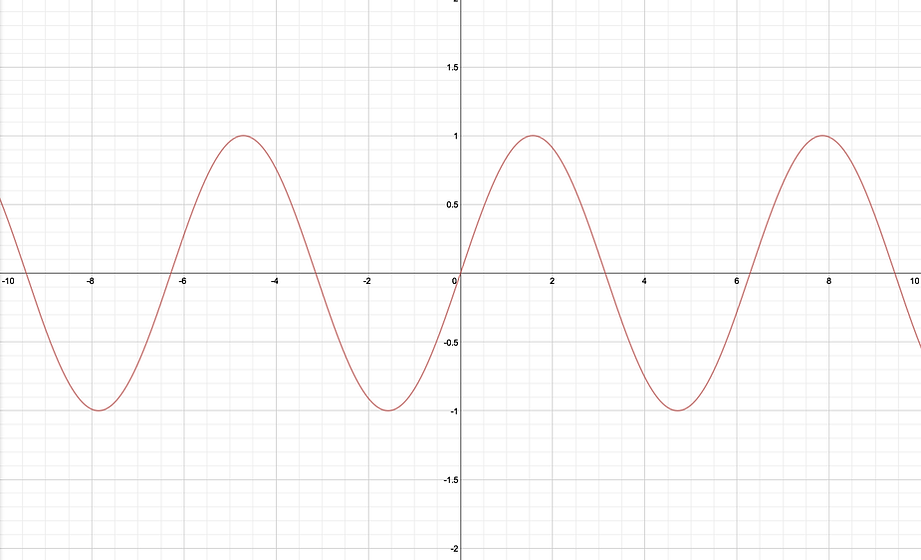
Now, cosine.
Cos is y value. Domain from 0 to π/2, x value is positive number, and it decreases. From π/2 to π, x is negative, and it still decreases. When x is from π to 3π/2, y value is still negative, but start increasing. From 3π/2 to 2π, it is positive value now and still increases. There is another animation.
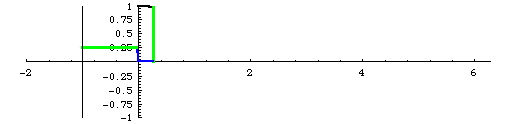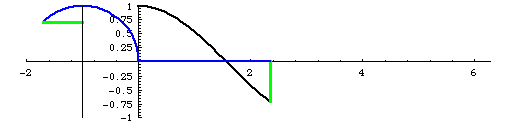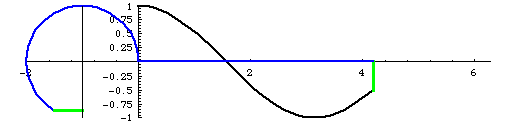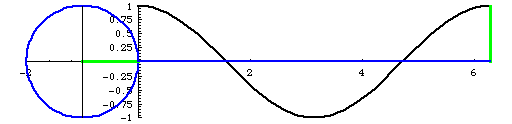
Tangent. Well, tan graph is harder to see straight away, because it isn't a value of x or y but the slope. Therefore, read the description very carefully, and draw the unit circle and graph in your mind.
First, when the angle is 0, the slope is also 0 because it is horizontal graph, constant function. What about π/4? It will make a isosceles right trangle, which means y=x, slope is 1. When the angle is almost, very close to π/2, but not π/2? The slope will be infinite because it is almost parallel with y-axis. However, when the angle is exactly π/2, it can't have slope because perpendicular line on graph is not a function. When the angle is slightly bigger than π/2, the slope is very small, and negative number. It will increase until 3π/2 (π will be 0 again), and undefined again when the angle is 3π/2.
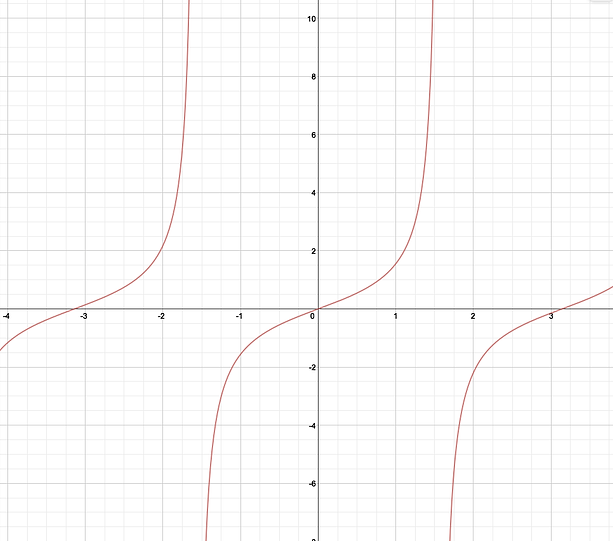
The graph looks like this. There is another way to understand. How can you find the slope of linear function? Rise over Run or change of y over change of x, right? When the angle is 0, y is 0 and x is 1. 0/1=1. When angle is π/4, x and y are same, √(2)/2, so the slope will be {√(2)/2}/{√(2)/2}=1. When angle is π, y is 1 and x is 0, so it is undefined. (we can't find the value that denominator is 0)
Analyzing the graph-period/amplitude-link
Trig Identities
There are some formulas you can get from trigonometry ratios.
We already know the pythagorean theorum works for the triangle we create on unit cicle because it is a right triangle. Also, we know that cos and sin is each x and y value, and also, the length of base and adjacement.
Pythagorean Theorum-h²=b²+p²
-----------
h=1
b=cosΘ
p=sinΘ
1²=cos²Θ+sin²Θ
-----------
We got one formula. 1²=cos²Θ+sin²Θ. From here, we can make some other formulas.
Divide the equation by cos²Θ. What happen?
What about divide by sin²Θ?
Finally, I got two more formulas.
1. sec²Θ = 1 + tan²Θ
2. csc²Θ = 1 + cot²Θ
Trigonometry in the real world
Trigonometry is actually using in the real world sometimes. The most common thing is find the height of very tall things, like building and mountain which can't easily be measured manually, or, find the distance between points far away from each other. However, it is also used for different formulas of different science fields.
TRIG MODELLING-temperature per month(link)
It is an example. Also, you can try questions below.
FINALLY, IT IS DONE!!!
I am pretty sure this is all about trigonometry now. There are deeper ones like calculus part and others, but...
If you have anything that want me to explain more or if you have any questions, please leave it on this page.
©Nyeong-Min Flora Lee
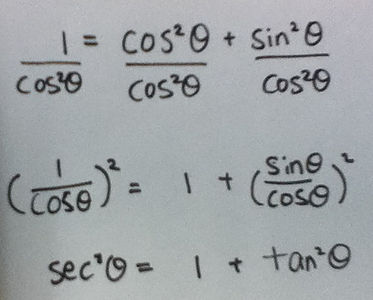


cos²Θ | it is same as (cosΘ)²