
Unit Cicle/Exact Trig Values
When we draw a right triangle on the plane coordinate, it is easy to get trigonometry ratios, especially for special angles. Draw a circle, radius of 1, center on the origin. This circle is called 'unit circle'. Then. choose any point on the circle. From that point, when you draw a straight segment to the origin. The length of it should be 1 because it is distance from a point on the circle to the center of the circle, the radius, 1. Then, draw a perpendicular line to the x-axis. Then, we get the right triangle, right? Let's call the angle between the radius and x-axis Θ. Also, we can find that the adjacent is x value of the point on the circle, and opposite is y. Now, we can find that;
-----------------------
sinΘ=y/1=y
cosΘ=x/1=x
tanΘ=y/x
-----------------------
What happen when Θ is 45º? Then, the triangle is isosceles right triangle, we can find x=y. Here, we can easily find x and y are all 1/√(2) or √(2)/2 because;
1²=x²+y²
1=2x²
1/2=x²
√(1/2)=x
x=1/√(2)=√(2)/2
We found x and y are 1/√(2) or √(2)/2. Here, we can find sinΘ and cosΘ, right? Because they are x and y. Simple!
*****
cos45º=1/√(2) or √(2)/2
sin45º=1/√(2) or √(2)/2
tan45º={1/√(2)}\{1/√(2)}=1
*****
What about Θ=30º?
Actually, this triangle is very interesing, so let's look closer.
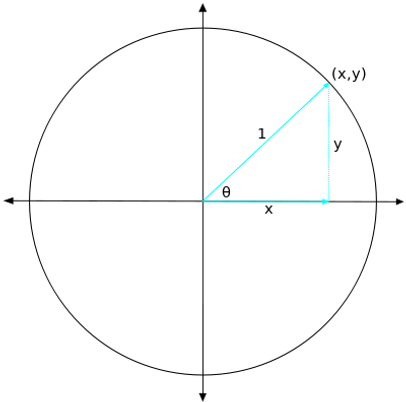
perpendicular | making a right angle, 90º. verticle
Angle smaller than 0º or greater than 360º | On the unit circle, you can see that the angle start from the positive side of x axis and move anticlockwise. Therefore, when the angle is over 360º, you just have to go around more times. For example, when it is 390º, go all the way of the circle once, and 30º more. Than, you can see 390º=30º. When the angle is negative, go backwords, clockwise. Remember it always STARTS FROM POSITIVE SIDE OF THE X-AXIS.

When you look at the image above, you can find triangle ABD the equaliteral triangle when you draw a line that cuts the right triangle for 60º and 30º. Also, you can find that the triangle BCD is isosceles triangle because two angles are same. Finally, we can find that length of all sides marked on the image is same. What can you see now? Can't you see that AC is double length of AB.
When you think the triangle is on the unit circle, with Θ=30º.
*****
1²=(1/2)²+BC²
1²-(1/2)²=BC²
(3/4)=BC²
√(3/4)=BC
√(3)/2=BC
*****
x=√(3)/2
y=1/2
hypothenus=1
By these values, we can easily find trig values.
-----------
sin30º=y=1/2
cos30º=x
=√(3)/2
tan30º=y/x=(1/2)/(√(3)/2)
=1/√(3)
=√(3)/3
-----------
Now, you can also find when Θ=60º because in that triangle above, one of the angle is 30º, but also the other one is 60º. The hypothenus is 1, as 30º. When you rotate the triangle a bit, you can easily find x and y values too.
x=1/2
y=√(3)/2
Just x and y will switch with Θ=30º. Then, what happen to sin and cos? They will just switch each other too!
------------
60º
sin60º=√(3)/2
cos60º=1/2
tan60º={1/2}/{√(3)/2}
=1/√(3)
=√(3)/3
------------
For further question solving and deeper studies, you have to memorize these values. Remember. When you add squares of sin and cos values, you have to get 1 (square of hypothenus).
If you have anything that want me to explain more or if you have any questions, please leave it on this page.